About the task
Presents two objects. One is correct and one is incorrect. If the subject touches the correct one, it is rewarded; if it touches the wrong one, it is punished. The discrimination varies in difficulty. The subject learns over several trials which stimuli are correct and which are incorrect; then we confuse it by changing the rules.
Stimuli can be simple (when they vary along only one dimension, such as shape, colour, intensity, or location), or compound (when they vary along more than one dimension).
Dimensional shifting in humans
In human testing, typical dimensions might be colour, shape, and number. A famous example of this kind of test is the Wisconsin Card Sorting Test, in which subjects must sort cards with a variable number of coloured shapes. They must discover the sorting rule solely by reinforcement from the experimenter. The rule is then changed: for example, they may be required to switch from "red correct, blue wrong" to "blue correct, red wrong" - a reversal. Alternatively, they may be given a new set of colours to learn - an intradimensional shift. Again, they may also be required to switch from "blue correct, red wrong" to "circles correct, squares wrong" - an extradimensional shift.
Dimensional shifting in non-human primates
In primate testing, two typical dimensions are "blue shapes" and "black squiggly lines". [See Dias R, Robbins TW, Roberts AC (1997). Dissociable forms of inhibitory control within prefrontal cortex with an analog of the Wisconsin Card Sort Test: restriction to novel situations and independence from "on-line" processing. Journal of Neuroscience 17: 9285-9297.] They use a large number of exemplars in each dimension (shapes and lines).
Basic test sequence in the general case
Assume there are two dimensions, A and B. There is a large catalogue of objects. Each object is assigned a value for each dimension (or is stated not to possess that dimension). For example, if the dimensions are colour and shape, then each object would be assigned a value for colour (e.g. "red") and shape (e.g. "triangle"). If there were a third dimension, of "superimposed wiggly line", a red triangle stimulus might have a value of "nonexistent" for this third dimension.
OK. For the sake of the following general prototype, keep in mind the primate tests in which the dimensions are typically "background shape" (values e.g. square, circle, triangle...) and "superimposed wiggly line" (similarly, with a variety of values).
| • | 1. Simple discrimination. Displayed objects possess dimension A but not dimension B. Within dimension A, value 1 is designated correct and value 2 is designated incorrect. In other words, we reward subjects if A()=1 and punish them if A()=2. (We can run this discrimination for as long as we can find target objects such that A(object)=1 and distractor objects such that A(object)=2, as long as in both cases B(object)=undefined.) |
| • | 2. Simple reversal. We carry on except that we now designate A()=1 as incorrect and A()=2 as correct. The subject has to reverse its responses to a previously-learned discrimination. |
| • | 3. Compound discrimination. We now introduce a second dimension, B, but ignore its value. Now objects are selected for presentation on the basis that ((A(object)=1 or A(object)=2) and B(object) != undefined). The symbol "!=" means "does not equal". The subject is rewarded if it selects an object such that A(object)=2 and are punished if they select an object such that A(object)=1. This continues the "A" discrimination from the previous, reversal stage. |
| • | 4. Reversal of compound discrimination. We reverse the discrimination along dimension A and continue to ignore B. The trials are just the same as the previous stage, but A()=1 is correct and A()=2 is incorrect once more. |
| • | 5. Intradimensional shift. We introduce new values of dimension A; dimension B is still ignored. Objects are selected such that ((A(object)=3 or A(object)=4) and B(object) != undefined). Subjects are rewarded if A(object)=3 and punished if A(object)=4. |
| • | 6. Extradimensional shift. We switch our attention to dimension B and ignore A. Objects are selected such that ((B(object)=1 or B(object)=2) and A(object) != undefined). Subjects are rewarded if B(response)=1 and punished if B(response)=2. |
What's ignored? By whom? A caveat. When a dimension B (or anything else) is present and being ignored, we would be wise to ensure that p(response is correct) is not dependent on the value of this dimension. Otherwise, our subject may well learn to discriminate on the dimension we (and it) are supposed to be ignoring. (Other dimensions like location or presentation order are important to consider here.) A dimension can be made irrelevant by holding the value of the dimension constant (e.g. always presenting stimuli in a single location, always making the background shape purple, etc.), or by randomizing it (e.g. always randomizing the locations of pairs of objects presented). If a dimension is randomized rather than held constant, the subject may attempt to learn the discrimination based on this dimension but cannot succeed.
Therefore, we need a library of objects with at least one object in each of the following categories:
A=1; B=undefined
A=2; B=undefined
A=1; B=anything except "undefined", constant or randomized
A=2; B=anything except "undefined", constant or randomized
A=3; B=anything except "undefined", constant or randomized
A=4; B=anything except "undefined", constant or randomized
A=anything except "undefined", constant or randomized; B=1
A=anything except "undefined", constant or randomized; B=2
Having lots of objects in each of these categories may be a good thing behaviourally, as it may lead the subject to extract the general features of that dimension/value (for example, if A(1) is equivalent to colour(red), then having lots of red objects may lead the subject to learn that "red" is correct, and not "red triangle"). This is the approach taken by the primate tasks, but not by tasks used for rats (or, now, pigs).
Dimensional shifting in rats
Birrell & Brown (2000) implemented a set-shifting task in rats (Birrell JM & Brown VJ, 2000. Medial frontal cortex mediates perceptual attentional set shifting in the rat. Journal of Neuroscience 20: 4320-4). Rats dug in two bowls for food. The bowls has dimensions of (A) odour; (B) filling medium; (C) surface texture. They adopted a policy of changing all stimuli at times of ID or ED shifting (a "total change design", p4321, which is required for accurate interpretation of the difference between reversal learning and ED shifts; see p4323). Their test sequence was as follows (+ indicates correct stimuli, - incorrect, bold indicates the correct part of the stimulus):
Simple discrimination |
A1(+), A2(-) |
Compound discrimination |
A1/B1(+), A2/B2(-) A1/B2(+), A2/B1(-) |
Reversal |
A2/B1(+), A1/B2(-) A2/B2(+), A1/B1(-) |
ID shift |
A3/B3(+), A4/B4(-) A3/B4(+), A4/B3(-) |
Reversal |
A4/B3(+), A3/B4(-) A4/B4(+), A3/B3(-) |
ED shift |
B5/A5(+), B6/A6(-) B5/A6(+), B6/A5(-) |
Reversal |
B6/A5(+), B5/A6(-) B6/A6(+), B5/A5(-) |
Dimensional shifting in pigs
In PigTab, Sidse wants the possible dimensions to be colour (which incorporates a dimension of luminance, or light intensity) and location (four possibilities in two pairs: left/right, up/down).
Therefore, a simple discrimination would be between two colours, or two spatial locations. But remember that for simple discriminations, dimension B must be undefined. Let's assume A() = colour() and B() = location(). Therefore, we cannot present two objects of different colours simultaneously, because then dimension B would be defined and irrelevant, not undefined. It would be a compound discrimination. Therefore, to use location as a dimension means that we have to present stimuli sequentially, not simultaneously. And that brings a problem: if the subject has to choose which of two sequential stimuli is correct, how is it to succeed? We can't just present one, then the other, because it might decide that the first one was correct only when it's seen the second. (Note that if you were to adopt a variant of this technique, you'd have to randomize presentation order as another potential dimension.) We can't present them both, then both simultaneously (because then location is present as a dimension on test!). We could alternate them until it makes a response, but this would bring in problems of interpretation if subjects differed in response latency/speed (either at baseline, or as the result of an experimental intervention). A test using location as a dimension and/or alternating stimuli would also be rendered incomparable to previous human, primate, and rat testing methods, none of which have used location as a dimension.
My conclusion: using location as a dimension in the test either (1) makes the distinction between simple and compound discrimination impossible, or (2) introduces a variety of practical and interpretative problems in designing the test environment. Therefore, I shall implement PigTab using a different dimension. Location shall be randomized.
What's best as the two dimensions? Could we use shape and colour? We'd have to define "absence of colour" - plausibly a black fill colour.
As to the sequence, let's adopt the Birrell & Brown (2000) sequence, adding a simple reversal and removing the ID reversal and the ED reversal as requested by Sidse (or making them optional).
The sequence used by PigTab
Simple discrimination |
A1(+), A2(-) |
Reversal |
A2(+), A1(-) |
Compound discrimination |
A1/B1(+), A2/B2(-) A1/B2(+), A2/B1(-) |
Reversal |
A2/B1(+), A1/B2(-) A2/B2(+), A1/B1(-) |
ID shift |
A3/B3(+), A4/B4(-) A3/B4(+), A4/B3(-) |
Reversal (optional) |
A4/B3(+), A3/B4(-) A4/B4(+), A3/B3(-) |
ED shift |
B5/A5(+), B6/A6(-) B5/A6(+), B6/A5(-) |
Reversal (optional) |
B6/A5(+), B5/A6(-) B6/A6(+), B5/A5(-) |
How long shall we test for? The usual measure on this task is trials (or errors) to criterion. Birrell & Bowman (2000) used a criterion of 6 consecutive correct correct responses. That seems reasonable (though make the number configurable).
Left/right position should be chosen randomly for each trial. Order of presentation of the two alternative pairs (e.g. which to present of A1/B1-A2/B2 or A1/B2-A2/B1) should be randomized in pairs of trials.
A technical issue: manufacturing compound stimuli
Compound stimuli can be designed by the user ("here's a shape; it has dimension attributes A3 and B4"), or assembled by the program (in some way, the user says "here are stimuli A1-A6 and B1-B6, please combine them as needed"). Now some attributes can only be created by the program (location would be one, but we're not going to use that). Which method is best? For shape/line combinations, it would seem more sensible for the program to assemble them. In the sequence shown above, the user would need to specify 12 stimuli (A1-6, B1-6) if the program does the combination, or 14 stimuli if the user does the combination (in total, 14 stimuli are shown in the sequence above).
That's not much of a difference, really. What other advantages do these two methods bring?
User generation means that the program could be used for any dimension conceived by the user - dimensions such as "which actor's in this photo" and "what colour house he's standing in front of", for example, which the program couldn't create.
Program generation means that the user has to generate fewer stimuli; this advantage becomes greater as the number of exemplars of each dimension increases. It means that dimensions are limited to things the program can generate. Superimposing visual stimuli is easy (and the basis of the program used by Dias et al., 1997). Changing the colour of a stimulus would be fairly easy (within PigTab's object generation system, this would mean the program iterating through all components of an object and forcing their brush fill settings to the chosen colour).
I think we should adopt user generation, as it's more flexible. For example, it's very easy to replace the stimulus set and perform a new dimensional shift assessment.
Configuring the task
Given that the user generates the stimuli, configuring the task is just a matter of plugging in the stimuli to the pattern shown above. That is, we need one object to correspond to each of A1, A2, A1/B1, A1/B2, A2/B1, A2/B2, A3/B3, A3/B4, A4/B3, A4/B4, A5/B5, A5/B6, A6/B5, A6/B6. Here's the configuration dialogue box:
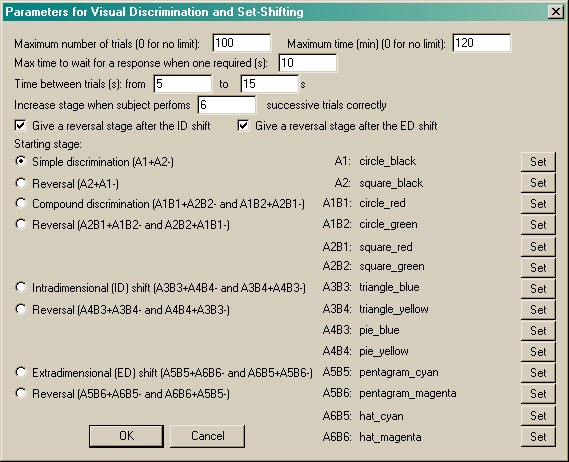
| • | Maximum number of trials. When the subject has performed this number of trials, the task ends. (You may specify 0 for no limit, though you must specify a limit on the number of trials, the time, or both.) |
| • | Maximum time. When this time elapses, the task is terminated as soon as the current trial has finished. (You may specify 0 for no limit, though you must specify a limit on the number of trials, the time, or both.) |
| • | Maximum time to wait for a response. If the subject fails to make a response within this time, the subject fails the trial. |
| • | Time between trials. Specify a minimum and a maximum intertrial time (they may be the same). The actual time is chosen with a rectangular probability distribution within these values. |
| • | Increase stage when subject performs X successive trials correctly. Fairly obvious, I hope. Set the value of X in the box. |
| • | Give a reversal stage after the ID shift. Enables/disables the "ID reversal" phase. |
| • | Give a reversal stage after the ED shift. Enables/disables the "ED reversal" phase. |
| • | Starting stage. Choose the stage to start at for this session. |
| • | Stimuli. Choose the stimuli required by the task (A1, A2, A1B1, etc.). An example is shown above, using shape and colour as dimensions A and B respectively. |
Screenshots of the task
