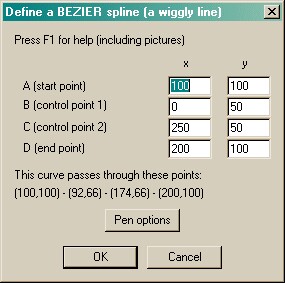
| • | The meaning of the points is explained in the figure above and in the examples and mathematical description below. |
| • | Click Pen options to determine how the edge of the object is painted. |
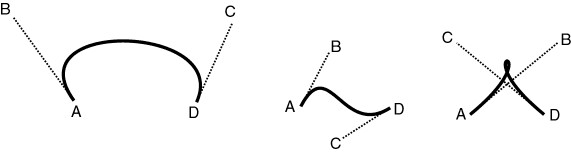
Some more examples:
Definition of a Bezier curve (de Casteljau, 1959; Bezier, 1962)
Let's start simple. Imagine a line that begins at A and ends at D. Let t be a variable from 0 to 1. We can define a point PAD(t) on the line segment AD as
PAD(t) = (1-t)A + tD
If we add another point, B, into the picture, we can define PAB(t) as a point between A and B, and PBD(t) as a point between B and D. If we apply the same method to define PAB-BD(t) as a point between PAB(t) and PBD(t), we get
PAB(t) = (1-t)A + tB
PBD(t) = (1-t)B + tD
PAB-BD(t) = (1-t){ (1-t)A + tB } + t{ (1-t)B + tD) } = (1-t)2A + 2t(1-t)B + t2D
This quadratic equation in t defines a quadratic Bezier curve - a parabola. For computer graphics purposes, cubic Bezier curves are more often used. As you might expect, these are defined by four points A, B, C, and D. If the cubic Bezier function is defined as a point between PAB-BC(t) and PBC-CD(t) in the same manner as we've been doing so far...
PAB(t) = (1-t)A + tB
PBC(t) = (1-t)B + tC
PCD(t) = (1-t)C + tD
PAB-BC(t) = (1-t){ (1-t)A + tB } + t{ (1-t)B + tC) } = (1-t)2A + 2t(1-t)B + t2C
PBC-CD(t) = (1-t){ (1-t)B + tC } + t{ (1-t)C + tD) } = (1-t)2B + 2t(1-t)C + t2D
CubicBezier(t) = (1-t)PAB-BC(t) + tPBC-CD(t) = ... = (1-t)3A + 3(1-t)2tB + 3(1-t)t2C + t3D
Summary: Where we end up
Cubic Bezier splines are usually defined with endpoints A and D and control points B and C that are not on the curve, as above. The equation for a point on this curve is given by
CubicBezier(t) = (1-t)3A + 3(1-t)2tB + 3(1-t)t2C + t3D
where t is the curve's parameter and ranges from 0 to 1. This curve can be expressed in a different way: as a curve passing through four points, PQRS, where P=CubicBezier(0), Q=CubicBezier(1/3), R=CubicBezier(2/3), and S=CubicBezier(1). From the formula above,
P = A
Q = 1/27(8A + 12B + 6C + D)
R = 1/27(A + 6B + 12C + 8D)
S = D
and therefore
A = P
B = 1/6(-5P + 18Q - 9R + 2S)
C = 1/6(2P - 9Q +18R - 5S)
D = S
In RatBat's Bezier dialogue box (above), you enter the points ABCD and RatBat shows you the points PQRS ("The curve passes through these points: ...").
Some properties of Bezier curves
| • | Bezier curves always pass through their first and last points (A and D here), but not necessarily through their other control points (B and C). |
| • | A Bezier curve always lies fully within the convex hull defined by its control points. |
| • | The line AB has the same tangent at the curve at A, and the line CD has the same tangent as the curve at D. |
| • | Bezier curves are always divisible into two Bezier curves (in a manner which makes them easy to draw iteratively). See Yuan, F. (2001), Windows Graphics Programming, Hewlett-Packard/Prentice Hall, New Jersey (p481 onwards). |