IN PROGRESS
Overview
This short guide is oriented towards those making the conversion from SPSS to R for ANOVA.
Analysis of variance in R is performed using one of the following methods, where depvar indicates the dependent variable and predictors is an expression describing the predictors (discussed below). Optional parameters (such as which data set to look for variables in) may also be necessary, but as a summary:
- aov(depvar ~ predictors), followed by summary() of the result to see a conventional ANOVA table. (The function "aov" is part of the "stats" package, and "summary" is part of "base".)
- lm(depvar ~ predictors) or glm(depvar ~ predictors), followed by anova() of the result. (All are part of the "stats" package.)
- The same underlying linear model (lm or some others), but using Anova() of the result; or, using Anova()'s additional ability to analyse within-subjects designs explicitly (and address sphericity questions). Anova (with a capital A) is part of the "car" (Companion to Applied Regression) package; it calculates Type-II or Type-III ANOVA tables.
- lme(depvar ~ predictors, furtherparameters) and then anova() of the result. Applicable to mixed models (fixed + random factors—in psychology, typically this equates to between + within-subjects factors) only. Also, this uses maximum likelihood (ML) or restricted maximum likelihood (REML) methods. It requires the "nlme" package; type library(nlme) to ensure it is active (see below if you get errors).
- lmer(depvar ~ predictors, furtherparameters) and then anova() of the result. Applicable to mixed models (fixed + random factors—in psychology, typically this equates to between + within-subjects factors) only. Also, this uses ML/REML techniques, as above. This requires the "lme4" package. Type library(lme4) to ensure it is active. If you receive the error message "Error in library(lme4) : there is no package called 'lme4'" when you do this, choose Packages > Install Packages from the R menus, choose a mirror site, and install the "lme4" package from the list (or, from the command line, install.packages("lme4") ).
- ezANOVA(dataframe, dv=.(depvar(s)), wid=.(subjectidentifier), within=.(withinsubjectvariable(s)), between=.(betweensubjectvariable(s)), otheroptions) encapsulates ANOVA but also validity checks (including Levene's test, Mauchly's test for sphericity, and the Greenhouse–Geisser and Huynh–Feldt epsilon corrections). It's very easy to use. It requires library(ez).
- Explicit model comparison: anova(reducedmodel, fullmodel).
Technicalities, or "make it look like SPSS"—how? Should we?
By default, R uses Type I sums of squares, and SPSS uses Type III sums of squares. What's the difference, and what's best?
-
What's the difference?
- The difference occurs when predictors are correlated. This can happen because (a) the predictors are correlated in the "real world" (e.g. you're predicting something using both age and blood pressure as predictors, and blood pressure tends to rise with age); or (b) the design is unbalanced (e.g. in an ANOVA with two factors A and B, each with two factors, the design is unbalanced if you don't have the same number of observations for A1B1, A1B2, A2B1, and A2B2 conditions).
- If the predictors are not correlated, then all the sums of squares add up neatly (in this two-factor example, SS[A] + SS[B] + SS[A*B] + SS[error] = SS[total]), and all ways of calculating the sums of squares are the same. The differences come when this is not the case. Let's look at a Venn diagram:
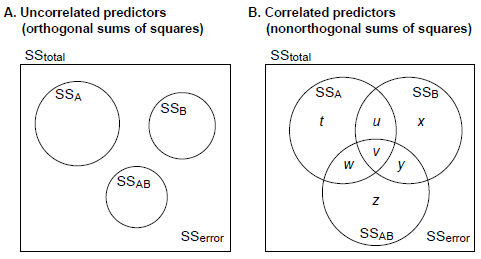
- Type I SS ("sequential"): Order-dependent. Assuming we put A first in the order, then SS[A] = t + u + v + w; SS[B] = x + y; SS[A*B] = z. This asks the questions: what's the whole effect of A (ignoring B)? What's the effect of B, over and above the effect of A? What's the effect of the A*B interaction, over and above the effects of A and B? These could be written as tests of A, and B|A, and AB|A,B.
- Type II SS ("hierarchical"): SS[A] = t + w; SS[B] = x + y; SS[A*B] = z. This adjusts terms for all other terms except higher-order terms including the same predictors (in this example, adjusting the main effects of A and B for each other, but not for the interaction); by "adjust for", we mean "not include any portion of the variance that overlaps with". These could be written as tests of A|B, and B|A, and AB|A,B.
- Type III SS ("marginal", "orthogonal"): SS[A] = t; SS[B] = x; SS[A*B] = z. This assesses the contribution of each predictor over and above all others. These could be written as tests of A|B,AB, and B|A,AB, and AB|A,B.
-
Which is best?
- If you have a hypothesis, perform the appropriate test for your hypothesis. (If not—why not?)
- All will give the same answer for the highest-order interaction (see the Venn diagram), so the question is how one should measure the effects of other factors (of the main effects of A and B, in the simple example in the Venn diagram).
- You rarely want Type I analysis. It's order-dependent (this being the only reason to use it: when one factor takes precedence over others theoretically). It's rarely useful in unbalanced designs (ref: Fox).
- The debate is usually between Type II and Type III. The differences are of power and assumptions.
- Type II: this is the most powerful when there's no interaction (look at the Venn diagram: bigger SS implies more power). A criticism is that the test for a given factor A assumes a negligible higher-order interaction involving A (such as AB). Others point out (though it's a slightly different point) that if the interaction is significant, then significant main effects are not of interest (interpreting main effects in the presence of an interaction is potentially fraught, though not always meaningless: see Cardinal & Aitken, 2006, section 3.7.1). So, an interpretation of Type II tests is as follows (Langsrud, 2003): "If a main effect is found to be significant, this result is correct if there is no interaction. If the interaction is present, both main effects will also be present. In any case, the statement about a significant main effect is correct." Langsrud argues that Type II tests are therefore correct, regardless of the presence of an interaction, and when there isn't an interaction, it's the most powerful, and therefore the best (BUT: see below re Myers & Well / Maxwell & Delaney). If there is an interaction, then there is no guarantee that the Type II is more powerful than the Type III method (it depends on the data), but it appears to be more powerful on average. Fox (2010) notes that Type II tests for A and B are "not tests of main effects in a reasonable interpretation of that term" if interactions are present.
- Type III: the usual reasons given for preferring this method is that it does not make the assumption that the interactions are negligible or non-existent (and so does not give biased effects of the main effects if there is an interaction). It is in some senses the most traditional (and therefore the default in many major statistical packages). Myers & Well (1995) advocate it as the best method for chance variation in the number of observations in each cell. They argue against the Type II method on the basis that weak (not very powerful) tests of the interaction may suggest that an interaction is absent—when in truth substantial variance is attributable to an interaction, thus leading to more type 1 errors for main effects (i.e. the test is too liberal: declaring main effects to be significant more often than one should). Myers & Well (2003, pp. 323, 626-629) and Maxwell & Delaney (2004, pp. 324-328, 332-335) expand on this point, noting that even interactions that do not approach significance can result in biased tests of the main effects. Howell (2009) is another advocate of the Type III method. The Type III SS approach has been criticized on grounds of power (e.g. Langsrud), on grounds of making assumptions that are not sensible (e.g. Langsrud), and of encouraging people to look at main effects in the presence of interactions (e.g. Venables)—such as examining main effects in the presence of an interaction, when the interaction caused the main effect in the first place. The Type III analysis requires violating the "marginality principle" that assumes that all terms to which a particular term is marginal are zero (lower-order terms are marginal to higher-order terms; thus, A and B are marginal to the interaction AB)—examining and reporting A and B requires, under the marginality principle, that we assume that the interaction AB is zero). To produce Type III tests, specific contrasts are needed (which you have to tell R about), or you can get garbage.
- Upshot: Use II or III. Use II for power (but beware over-liberal tests for main effects with no interaction, and take care as always regarding the interpretation of main effects in the presence of an interaction). Use type III for conservative safety (regarding main effects). Whichever you pick, there are statisticians who will support your general approach!
- Personal suggestion (Jan 2011): use an extension to ezANOVA with the type="III" option.
-
What do SPSS and R do?
- SPSS can do any of these, though it defaults to Type III.
-
R can do any of these.
- The summary(aov(...)) and anova(lm(...)) commands default to Type I (and need the drop1 command to get to Type III, which works as long as appropriate sum-to-zero contrasts have been specified e.g. with options(contrasts=c(unordered="contr.sum", ordered="contr.poly"))).
- Anova (with a capital A) defaults to Type II, but can use Type III simply by specifying this as an option (as long as you've set sum-to-zero contrasts).
- ezANOVA uses Type II (as of Jan 2011) via calls to car::Anova(), occasionally falling back (with a warning) to stats::aov, which uses Type I. For a modification that allows Type III SS as an option, and makes the dropping-to-Type-I warning more explicit, see extensions.
- lme defaults to type I (type="sequential") but can be switched to type III with anova( lme(...), type="marginal").
Prerequisites
See Entering data and Saving and loading for details of how to get data into a data frame.
The most generally useful format (for communication with data sources such as relational databases, etc.) is "long" format data frames, in which each row equates to one observation. R also likes this format. See Reshaping data frames for more details. We'll assume "long" format unless otherwise specified.
Prerequisites for individual functions:
library(ez) # for any of the ez* functions
Prerequisites for test data used in this page: see test code below.
Quick data summaries
Structure:
ezPrecis(dataframe)
Between-subjects means, SDs, and Fisher's LSD:
ezStats(dataframe,
dv=.(depvar(s)),
wid=.(subjectidentifier),
within=.(withinsubjectvariable(s)),
between=.(betweensubjectvariable(s)), otheroptions)
Means, if you use the aov analysis command:
fit <- aov(...something...)
model.tables(fit, "means")
# or of effects (differences from the overall mean(s)):
model.tables(fit, "effects")
Quick diagnostics (e.g. residuals plots), if you use the aov analysis command:
fit <- aov(...something...)
plot(fit)
Quick visualization
# Only basic syntax given; see ?ezPlot for more. Not all options are required.
ezPlot(dataframe, dv=.(depvar(s)), wid=.(subjectidentifier), within=.(withinsubjectvariable(s)), between=.(betweensubjectvariable(s)),
x=.(X-axis variable), x_lab=X-axis_label,
y_lab=X-axis_label,
split=.(variable to split data by (shapes/colours/line type)), split_lab=key_labels_for_splitting,
row=.(variable to split data into rows of graphs by), col=.(variable to split data into columns of graphs by),
do_lines=whether_to_connect_with_lines, do_bars=whether_to_plot_error_bars
)
The designs
The numbering follows chapter 8 of Cardinal & Aitken (2006). We use depvar for the dependent variable, A, B, ... for between-subjects factors, S for subjects, U, V, ... for within-subjects factors, and Xdetails for continuous covariates.
8.1 One between-subjects (BS) factor
Alternative names: one-way ANOVA; completely randomized design (CRD).
There are several ways to do the syntax in R. I'll highlight the ezANOVA one, since this translates easily to more complex designs.
# Lots of ways... here are a few. "data1" is my data frame.
ezANOVA(data1, dv=.(depvar), wid=.(S), between=.(A), detailed=TRUE)
anova( aov(depvar ~ A, data=data1) )
anova( lm(depvar ~ A, data=data1) )
Anova( lm(depvar ~ A, data=data1) )
Cross-comparison to SPSS 17 with:
UNIANOVA depvar BY A
/METHOD=SSTYPE(3)
/INTERCEPT=INCLUDE
/PRINT=HOMOGENEITY
/CRITERIA=ALPHA(.05)
/DESIGN=A.
The cross-comparison gives identical results for the ANOVA. SPSS (with this option) produces Levene's test with slightly different statistics to R with the syntax shown above; this is because SPSS defaults to the "mean-centred" version of Levene's test, while R (car and ezANOVA packages alike) defaults to the "median-centred" version, which is (a) usually more robust, and (b) strictly called the Brown–Forsythe test; see these NIST and Wikipedia pages for explanations. To get the same version of Levene's test that SPSS uses, you can use this syntax:
leveneTest(depvar~A, data=dataframe, center=mean) # Levene's test in its original form. This function is in the car library (car::leveneTest).
ezANOVA(data1, dv=.(depvar), wid=.(S), between=.(A), detailed=TRUE, levenecenter="mean") # if you use my hacked version of ezANOVA
8.2 Two BS factors
Alternative names: two-way ANOVA; factorial ANOVA; a × b factorial ANOVA (where a and b are the number of levels of factors A and B; for example, a "2 × 5 factorial" has one factor with 2 levels and a second factor with 5 levels); factorial, completely randomized design ANOVA.
R methods include:
# Type II SS
ezANOVA(data2, dv=.(depvar), wid=.(S), between=.(A,B), detailed=TRUE)
# Type III SS
ezANOVA(data2, dv=.(depvar), wid=.(S), between=.(A,B), detailed=TRUE, type="III", levenecenter="mean")
# Yet more methods...
with(data2, {
# aov / anova : Type I : A*B
anova( aov(depvar ~ A*B) )
# aov / anova : Type I : B*A (different answer - different model order)
anova( aov(depvar ~ B*A) )
# lm / anova : Type I: A*B
anova( lm(depvar ~ A*B) )
# lm / anova : Type I: B*A (different answer to the previous - different model order)
anova( lm(depvar ~ B*A) )
# lm / Anova, default option : Type II
Anova( lm(depvar ~ A*B) )
# CRUD FOLLOWS: if your output matches that of what follows, the wrong contrasts are set in the attempt to get Type III output
# If you use the drop1() command below without setting any options, you'll get rubbish, because "contr.treatment" is the default when R starts
cat("WARNING: THE NEXT ONE IS RUBBISH!\n")
options(contrasts=c("contr.treatment", "contr.poly")); drop1( aov(depvar ~ A*B), ~., test="F" )
cat("WARNING: THE ONE ABOVE IS RUBBISH!\n")
# sum-to-zero contrasts / aov / drop1 : Type III (correctly!)
options(contrasts=c("contr.sum", "contr.poly")); drop1( aov(depvar ~ A*B), ~., test="F" )
# sum-to-zero contrasts / lm / Anova, with Type III option (correctly!)
options(contrasts=c("contr.sum", "contr.poly")); Anova( lm(depvar ~ A*B), type="III" )
}
Cross-comparison of the type III method (e.g. with ezANOVA) to SPSS 17 gives identical output (using the "levenecenter=mean" option if you want to use Levene's original test, like SPSS does) to the following SPSS syntax:
UNIANOVA depvar BY A B
/METHOD=SSTYPE(3)
/INTERCEPT=INCLUDE
/PRINT=HOMOGENEITY
/CRITERIA=ALPHA(.05)
/DESIGN=A B A*B.
8.3 Three BS factors
Alternative names: a × b × c factorial ANOVA (where a, b, and c are the number of levels of factors A, B, and C; for example, a "2 × 5 × 3 factorial" has three factors with 2, 5, and 3 levels, respectively); factorial, completely randomized design ANOVA.
R: e.g.
# Compare to 2 BS factors. I'll just illustrate the ezANOVA syntax here.
# Type II
ezANOVA(data3, dv=.(depvar), wid=.(S), between=.(A,B,C), detailed=TRUE, type="II")
# Type III
ezANOVA(data3, dv=.(depvar), wid=.(S), between=.(A,B,C), detailed=TRUE, type="III")
Cross-comparison (of ezANOVA / type III SS / Levene's test centred on the mean) gives identical output to SPSS 17 with this syntax:
UNIANOVA depvar BY A B C
/METHOD=SSTYPE(3)
/INTERCEPT=INCLUDE
/PRINT=HOMOGENEITY
/CRITERIA=ALPHA(.05)
/DESIGN=A B C A*B A*C B*C A*B*C.
8.4 One within-subjects (WS) factor
Alternative names: repeated-measures ANOVA (with one factor); randomized complete block (RCB) design (with one factor); single-factor within-subjects design.
Simplest R method (type II/III SS being equivalent as this design is necessarily balanced, given the prerequisite of all subjects being measured in all conditions, so the "type" specification is redundant):
ezANOVA(data4, dv=.(depvar), wid=.(S), within=.(U), detailed=TRUE)
# But for the masochists, also:
summary(aov(depvar ~ U + Error( S/U ), data=data4 ) ) # Direct long-format analysis; no sphericity analysis/corrections
summary( Anova( lm(formula = cbind(U1, U2, U3) ~ 1, data=data4wide), # direct wide-format analysis
idata = data.frame( U = factor(1:3) ), # the idata data frame must have (1) rows that, in order, each represent a column in the data frame being analysed by the lm; (2) columns that are the within-subjects factors
idesign = ~U ) )
# lme - IN PROGRESS
# lmer - IN PROGRESS
SPSS equivalents (same as R ezANOVA output including Mauchly/Huynh–Feldt/Greenhouse–Geisser):
/* wide format (standard) */
GLM U1 U2 U3
/WSFACTOR=U 3 Polynomial
/METHOD=SSTYPE(3)
/CRITERIA=ALPHA(.05)
/WSDESIGN=U.
/* Unconventional long format analysis (omits sphericity analysis/corrections): */
UNIANOVA depvar BY U S
/RANDOM=S
/METHOD=SSTYPE(3)
/INTERCEPT=INCLUDE
/CRITERIA=ALPHA(0.05)
/DESIGN=S U.
/* Could also use this - same answer - but no value given for S(ubject)*U interaction, as this is confounded with error: */
UNIANOVA depvar BY S U
/RANDOM=S
/METHOD=SSTYPE(3)
/INTERCEPT=INCLUDE
/CRITERIA=ALPHA(0.05)
/DESIGN=S U S*U.
/* No Levene's test: no between-subjects factors */
8.5 Two WS factors
Alternative names: repeated-measures ANOVA (with two factors); randomized complete block (RCB) design (with two factors); two-factor within-subjects design; split-block design.
R methods:
# Design necessarily balanced so "type" specification redundant (delete a subject: remains balanced; delete an observation: won't analyse, just like SPSS Repeated Measures)
ezANOVA(data5, dv=.(depvar), wid=.(S), within=.(U,V), detailed=TRUE)
# or, the harder ways: (1) direct analysis of long-format data (no sphericity analysis/corrections)...
summary(aov(depvar ~ U * V + Error( S/(U*V) ), data=data5 ) )
# ... and direct wide-format analysis (gives sphericity corrections):
summary( Anova( lm(formula = cbind(U1V1, U1V2, U1V3, U2V1, U2V2, U2V3) ~ 1, data=data5wide),
idata = data.frame( U = factor(c(1,1,1,2,2,2)), V = factor(c(1,2,3,1,2,3)) ),
idesign = ~U*V ) )
# lme - IN PROGRESS
# lmer - IN PROGRESS
R's ezANOVA methods give the same output as the following SPSS syntax:
/* wide format (standard) */
GLM U1V1 U1V2 U1V3 U2V1 U2V2 U2V3
/WSFACTOR=U 2 Polynomial V 3 Polynomial
/METHOD=SSTYPE(3)
/CRITERIA=ALPHA(.05)
/WSDESIGN=U V U*V.
/* Unconventional long format analysis (omits sphericity analysis/corrections) - full model; same answer as previous syntax: */
GLM depvar BY U V S
/RANDOM=S
/METHOD=SSTYPE(3)
/INTERCEPT=INCLUDE
/CRITERIA=ALPHA(0.05)
/DESIGN=U V S U*V U*S V*S U*V*S.
/* Other models exist; see e.g. Cardinal & Aitken 2006. */
/* No Levene's test: no between-subjects factors */
8.6 Three WS factors
Alternative names: repeated-measures ANOVA (with three factors); randomized complete block (RCB) design (with three factors); three-factor within-subjects design.
R methods:
# Design necessarily balanced so "type" specification redundant (delete a subject: remains balanced; delete an observation: won't analyse, just like SPSS Repeated Measures)
ezANOVA(data6, dv=.(depvar), wid=.(S), within=.(U,V,W), detailed=TRUE)
# Or the harder ways: (1) direct long-format analysis (sphericity assumed):
summary(aov(depvar ~ U * V * W + Error( S/(U*V*W) ), data=data6 ) )
# ... (2) direct wide-format analysis with car::Anova:
summary( Anova( lm(formula = cbind(U1V1W1, U1V1W2, U1V1W3, U1V2W1, U1V2W2, U1V2W3, U1V3W1, U1V3W2, U1V3W3, U2V1W1, U2V1W2, U2V1W3, U2V2W1, U2V2W2, U2V2W3, U2V3W1, U2V3W2, U2V3W3) ~ 1, data=data6wide),
idata = data.frame( U = factor(rep(1:2,each=9)), V = factor(rep(1:3,each=3,times=2)), W = factor(rep(1:3,times=6)) ),
idesign = ~U*V*W,
type = "III" ) )
# lme - IN PROGRESS
# lmer - IN PROGRESS
R's ezANOVA methods give the same output as the following SPSS syntax:
/* wide format (standard) */
GLM U1V1W1 U1V1W2 U1V1W3 U1V2W1 U1V2W2 U1V2W3 U1V3W1 U1V3W2 U1V3W3 U2V1W1 U2V1W2 U2V1W3 U2V2W1
U2V2W2 U2V2W3 U2V3W1 U2V3W2 U2V3W3
/WSFACTOR=U 2 Polynomial V 3 Polynomial W 3 Polynomial
/METHOD=SSTYPE(3)
/CRITERIA=ALPHA(.05)
/WSDESIGN=U V W U*V U*W V*W U*V*W.
/* Unconventional long format analysis (omits sphericity analysis/corrections) - full model; same answer as previous syntax - slow execution!: */
GLM depvar BY U V W S
/RANDOM=S
/METHOD=SSTYPE(3)
/INTERCEPT=INCLUDE
/CRITERIA=ALPHA(0.05)
/DESIGN=U V W S U*V U*W U*S V*W V*S W*S U*V*W U*V*S U*W*S V*W*S U*V*W*S.
/* Other models exist; see e.g. Cardinal & Aitken 2006. */
/* No Levene's test: no between-subjects factors */
8.7 One BS and one WS factor
Alternative names: split-plot design; mixed two-factor within-subjects design; repeated measures analysis using a split-plot design; univariate mixed models approach with subject as a random effect.
Our first mixed model. R methods:
# Type II
ezANOVA(data7, dv=.(depvar), wid=.(S), between=.(A), within=.(U), detailed=TRUE, type="II")
# Type III
ezANOVA(data7, dv=.(depvar), wid=.(S), between=.(A), within=.(U), detailed=TRUE, type="III")
# The harder ways, as before:
summary(aov(depvar ~ A * U + Error( S/U ), data=data7 ) ) # long-format analysis;
# BEWARE - provides TYPE I SS (= TYPE II SS IN THIS PARTICULAR DESIGN, as BS/WS factors are always dealt with asymetrically - aov() calls lm() separately for each stratum);
# drop1() command can't be used on the aov() result in this case
# "aov() is designed for balanced designs, and the results can be hard to interpret without balance" - from ?aov - so avoid.
summary( Anova( lm(formula = cbind(U1, U2, U3) ~ A, data=data7wide),
idata = data.frame( U = factor(1:3) ),
idesign = ~U,
type = "III" )
# lme - IN PROGRESS
# lmer - IN PROGRESS
R's ezANOVA methods give the same output as the following SPSS syntax, except that ezANOVA doesn't give Levene's test for U1/U2/U3 across levels of A—but you can always do this with leveneTest(U1~A, data=data7wide, center="mean"), or leveneTest(depvar~A, data=data7[data7$U=="U1",], center="mean"), and similarly for other levels of U.
/* wide format (standard) */
GLM U1 U2 U3 BY A
/WSFACTOR=U 3 Polynomial
/METHOD=SSTYPE(3)
/PRINT=HOMOGENEITY
/CRITERIA=ALPHA(.05)
/WSDESIGN=U
/DESIGN=A.
/* Unconventional long format analysis (omits sphericity analysis/corrections) - full model; THIS ONE NEEDS MANUAL EDITING, NOT THE DEFAULT FROM THE SPSS MENUS; same answer as previous syntax - slow execution!: */
GLM depvar BY A U S
/RANDOM=S
/METHOD=SSTYPE(3)
/INTERCEPT=INCLUDE
/CRITERIA=ALPHA(.05)
/DESIGN=A S(A) U U*A. /* Including a U*S(A) term is sometimes done - see Cardinal & Aitken (2006) - SPSS default (via its Repeated Measures [wide] mode) is not to */
8.8 Two BS factors and one WS factor
R methods:
# Type II
ezANOVA(data8, dv=.(depvar), wid=.(S), between=.(A,B), within=.(U), detailed=TRUE, type="II")
# Type III
ezANOVA(data8, dv=.(depvar), wid=.(S), between=.(A,B), within=.(U), detailed=TRUE, type="III")
# And now the more complex methods start to become a bit pointless.
# First, aov: the problem is that this provides Type I SS (so analysing A*B*U differs from analysing B*A*U), and the drop1() command doesn't like the multi-stratum output from aov().
# summary(aov(depvar ~ A * B * U + Error( S/U ), data=data8 ) ) # BEWARE, as above.
# summary(aov(depvar ~ B * A * U + Error( S/U ), data=data8 ) ) # BEWARE, as above.
# Next, car::Anova(), but that's what ezANOVA uses, so there's little point:
summary( Anova( lm(formula = cbind(U1, U2, U3) ~ A*B, data=data8wide),
idata = data.frame( U = factor(1:3) ),
idesign = ~U,
type = "III" ) )
# lme - IN PROGRESS
# lmer - IN PROGRESS
R ezANOVA output matches the following SPSS syntax (you can add Levene's test by hand, exactly as in 8.7 above):
/* wide format (standard) */
GLM U1 U2 U3 BY A B
/WSFACTOR=U 3 Polynomial
/METHOD=SSTYPE(3)
/PRINT=HOMOGENEITY
/CRITERIA=ALPHA(.05)
/WSDESIGN=U
/DESIGN=A B A*B.
/* Unconventional long format analysis (omits sphericity analysis/corrections) - full model; THIS ONE NEEDS MANUAL EDITING, NOT THE DEFAULT FROM THE SPSS MENUS; same answer as previous syntax - slow execution!: */
GLM depvar by A B S U
/RANDOM = S
/METHOD=SSTYPE(3)
/INTERCEPT=INCLUDE
/CRITERIA=ALPHA(.05)
/DESIGN = A B A*B S(A*B) U U*A U*B U*A*B. /* Including a U*S*(A*B) term is sometimes done - see Cardinal & Aitken (2006) - SPSS default (via its Repeated Measures [wide] mode) is not to */
8.9 One BS factor and two WS factors
R methods:
# Type II
ezANOVA(data8, dv=.(depvar), wid=.(S), between=.(A), within=.(U,W), detailed=TRUE, type="II")
# Type III
ezANOVA(data8, dv=.(depvar), wid=.(S), between=.(A), within=.(U,W), detailed=TRUE, type="III")
# The following also gives type I/II SS (in this particular case equivalent - each term analysed in its own error stratum), from the long-format data:
summary(aov(depvar ~ A * U * V + Error( S/(U*V) ), data=data9 ) )
# The following just does what ezANOVA does, using the wide format data directly:
summary( Anova( lm(formula = cbind(U1V1, U2V1, U3V1, U1V2, U2V2, U3V2) ~ A, data=data9wide),
idata = data.frame( U = factor(rep(1:3,times=2)), V = factor(rep(1:2,each=3) ) ),
idesign = ~U*V,
type = "III" ) )
# lme - IN PROGRESS
# lmer - IN PROGRESS
R ezANOVA output matches the first SPSS syntax shown below. You can add Levene's test using leveneTest(U1V1~A, data=data9wide, center="mean"), or leveneTest(depvar~A, data=data9[data9$U=="U1" & data9$V=="V1",], center="mean"), and similarly for other combinations of levels of U and V.
/* wide format (standard) */
GLM U1V1 U1V2 U2V1 U2V2 U3V1 U3V2 BY A
/WSFACTOR=U 3 Polynomial V 2 Polynomial
/METHOD=SSTYPE(3)
/PRINT=HOMOGENEITY
/CRITERIA=ALPHA(.05)
/WSDESIGN=U V U*V
/DESIGN=A.
/* NOTE THAT BOTH "LONG" FORMS BELOW CAN GIVE VERY SLIGHT DIFFERENCES TO THE SPSS SYNTAX ABOVE - */
/* - for our sample unbalanced dataset (data9/data9wide), for example, though not for the balanced Myers&Well1995p313 dataset. */
/* Am not exactly sure yet where the difference lies. And both forms below can give different answers to each other. */
/* The differences are for SS(U) and SS(V). */
/* Unconventional long format analysis (omits sphericity analysis/corrections) - NOTE CAVEAT ABOVE */
GLM depvar BY A S U V
/RANDOM=S
/METHOD=SSTYPE(3)
/INTERCEPT=INCLUDE
/PRINT=HOMOGENEITY
/CRITERIA=ALPHA(.05)
/DESIGN=A S(A) U U*A U*S(A) V V*A V*S(A) U*V U*V*A.
/* Unconventional long format analysis (omits sphericity analysis/corrections) - NOTE CAVEAT ABOVE */
GLM depvar BY A S U V
/RANDOM=S
/METHOD=SSTYPE(3)
/INTERCEPT=INCLUDE
/PRINT=HOMOGENEITY
/CRITERIA=ALPHA(.05)
/DESIGN=A S(A) U U*A U*S(A) V V*A V*S(A) U*V U*V*A U*V*S(A).
8.10 Other ANOVA designs with BS and/or WS factors
These should now be self-explanatory, at least with the ezANOVA command, which does most of the work for you.
8.11 One BS covariate (linear regression)
Alternatives names: linear regression; analysis of covariance (ANCOVA)—although traditionally this term isn't applied to a design with no other factors.
R makes linear regression very, very simple. R methods:
with(data11, plot(X, depvar) ) # plot the data
fit11.lm <- lm(depvar ~ X, data=data11) # create the linear model, and store it in a variable so we can play with it easily. That's it for the actual regression! The rest is exploration of it:
fit11.lm # prints model (with intercept and slope)
summary(fit11.lm) # prints residual quantiles, coefficients (with t tests), r-squared, overall F test
anova(fit11.lm) # one way to show the ANOVA table (but not the coefficients)
Anova(fit11.lm) # and another
plot(fit11.lm) # plot some diagnostics (residuals v. fitted values; residual Q-Q plot; scale–location plot; residuals v. leverage plot)
Equivalent SPSS syntax:
/* A bunch of ways, of course... here are two. */
REGRESSION
/MISSING LISTWISE
/STATISTICS COEFF OUTS R ANOVA
/CRITERIA=PIN(.05) POUT(.10)
/NOORIGIN
/DEPENDENT depvar
/METHOD=ENTER X.
UNIANOVA depvar WITH X
/METHOD=SSTYPE(3)
/INTERCEPT=INCLUDE
/CRITERIA=ALPHA(.05)
/DESIGN=X.
8.12 One BS covariate and one BS factor
Reminding ourselves of what an interaction means in this context (one is present in data12b but not in data12a) (see Cardinal & Aitken 2006 for more discussion):
# Plotting our two example datasets:
with(data12a, plot(X, depvar, pch=ifelse(A=="A1","*","o")) ) # plot data with symbols indicating A group membership
with(data12b, plot(X, depvar, pch=ifelse(A=="A1","*","o")) ) # plot data with symbols indicating A group membership
8.12.1 The covariate and factor do not interact
Alternative names: analysis of covariance (ANCOVA); analysis of covariance (ANCOVA) assuming homogeneity of regression; traditional ANCOVA.
R methods:
fit12a.lm.nointeraction <- lm(depvar ~ X + A, data=data12a)
# Now print the model directly, and/or use summary() and/or Anova() to show the output.
# BEWARE anova() AT THIS POINT: analysing lm(depvar ~ X + A) gives different results from analysing lm(depvar ~ A + X), since anova() uses type I SS.
# If you do want an ordered (type I) model, anova() gives priority to the earlier terms in the list (i.e. "A + X" prioritizes A over X).
# Unless you want to specify an ordered model (and you might!), choose II or III. For example:
Anova(fit12a.lm.nointeraction, type="III")
# The t-tests that come from summary() are not order-dependent, and appear to be equivalent to Anova(,"type III") output.
# Regarding intercepts in linear models:
# lm() itself doesn't care whether you use "depvar ~ 1 + X + A" or "depvar ~ X + A" - it includes an intercept term whether or not you specify it.
# To get rid of an intercept term (why??) you'd have to call lm() with "depvar ~ 0 + X + A".
Default ANOVA-style SPSS syntax, equivalent to the Anova(,type="III") command shown above:
UNIANOVA depvar BY a WITH x
/METHOD = SSTYPE(3)
/INTERCEPT = INCLUDE
/CRITERIA = ALPHA(.05)
/DESIGN = x a.
8.12.2 The covariate and factor interact
Alternative names: analysis of covariance (ANCOVA) allowing covariate × factor interaction; analysis of covariance (ANCOVA): full model to check homogeneity of
regression; homogeneity-of-slopes design ANCOVA.
R methods:
fit12b.lm.interaction <- lm(depvar ~ X * A, data=data12b)
# Now use summary(), or Anova(..., type="III"), or whatever other method you prefer (as above), to show the output.
Equivalent SPSS syntax, as before:
UNIANOVA depvar BY a WITH x
/METHOD = SSTYPE(3)
/INTERCEPT = INCLUDE
/CRITERIA = ALPHA(.05)
/DESIGN = x a x*a.
8.13 One BS covariate and two BS factors
Alternative names: factorial analysis of covariance (factorial ANCOVA).
R methods:
# Assuming no factor x covariate interactions (just the factor x factor interaction):
fit13.lm <- lm(depvar ~ X + A*B, data=data13)
summary(fit13.lm)
Anova(fit13.lm, type="III")
# Quick and dirty way of showing group membership on a plot for this example (two factors each with two levels, plus one covariate):
with(data13, plot(X, depvar, pch=ifelse(A=="A1",ifelse(B=="B1","*","o"),ifelse(B=="B1","X","+")) )) # plot data with symbols indicating A/B group membership
Equivalent SPSS syntax:
UNIANOVA
depvar BY a b WITH x
/METHOD = SSTYPE(3)
/INTERCEPT = INCLUDE
/CRITERIA = ALPHA(.05)
/DESIGN = x a b a*b
8.14 Two or more BS covariates (multiple regression)
Alternative names: multiple regression; multiple linear regression.
R methods (interactions are not included in this example, as is typical):
fit14.lm <- lm(depvar ~ X1 + X2 + ..., data=data14)
summary(fit14.lm)
Anova(fit14.lm, type="III")
# If you want an ordered model (type I SS):
anova(fit14.lm)
Equivalent SPSS syntax (a couple of versions):
REGRESSION
/MISSING LISTWISE
/STATISTICS COEFF OUTS R ANOVA
/CRITERIA=PIN(.05) POUT(.10)
/NOORIGIN
/DEPENDENT depvar
/METHOD=ENTER x1 x2.
UNIANOVA depvar WITH x1 x2
/METHOD = SSTYPE(3)
/INTERCEPT = INCLUDE
/CRITERIA = ALPHA(.05)
/DESIGN = x1 x2.
8.15 Two or more BS covariates and one or more BS factors
Alternative names: factorial analysis of covariance (factorial ANCOVA) with multiple covariates.
R methods (for the example of two covariates X1 and X2, and two factors A and B; the factors are allowed to interact with each other but not with the covariates in this example):
fit15.lm <- lm(depvar ~ X1 + X2 + A*B, data=data15)
summary(fit15.lm)
Anova(fit15.lm, type="III")
Equivalent SPSS syntax:
UNIANOVA
depvar BY a b WITH x1 x2
/METHOD = SSTYPE(3)
/INTERCEPT = INCLUDE
/CRITERIA = ALPHA(.05)
/DESIGN = x1 x2 a b a*b .
8.16 One WS covariate
Alternative names: multiple regression with the covariate and Subject as predictors.
R methods:
fit16.lm = lm(depvar ~ X + S, data=data16) # Note: S not explicitly treated as random. However, gives correct answer in Bland & Altman/Boyd sample data; RECHECK THEORETICALLY ***.
fit16.lm # prints the linear model, with its coefficients (= b values), including that for X
summary(fit1.lm) # prints the summary (including coefficients) and t tests
Anova(fit1.lm, type="III") # shows it as an ANOVA table
# lme - IN PROGRESS
# lmer - IN PROGRESS
Equivalent SPSS syntax:
UNIANOVA depvar BY s WITH x
/RANDOM = s
/METHOD = SSTYPE(3)
/PRINT = PARAMETER
/INTERCEPT = INCLUDE
/CRITERIA = ALPHA(.05)
/DESIGN = x s.
8.17 One WS covariate and one BS factor
R methods:
***
Equivalent SPSS syntax:
***
8.17.1 The covariate and factor do not interact
R methods:
***
Equivalent SPSS syntax:
***
8.17.2 The covariate and factor interact
R methods:
***
Equivalent SPSS syntax:
***
8.18 Hierarchical designs
R methods:
***
Equivalent SPSS syntax:
***
8.18.1 Subjects within groups within treatments (S/G/A)
R methods:
***
Equivalent SPSS syntax:
***
8.18.2 Groups versus individuals
R methods:
***
Equivalent SPSS syntax:
***
8.18.3 Adding a further within-group, BS variable (S/GB/A)
R methods:
***
Equivalent SPSS syntax:
***
8.18.4 Adding a within-subjects variable (US/GB/A)
R methods:
***
Equivalent SPSS syntax:
***
8.18.5 Nesting within-subjects variables, such as V/US/A
R methods:
***
Equivalent SPSS syntax:
***
8.18.6 The split-split plot design
R methods:
***
Equivalent SPSS syntax:
***
8.18.7 Three levels of relatedness
R methods:
***
Equivalent SPSS syntax:
***
8.19 Latin square designs
R methods:
***
Equivalent SPSS syntax:
***
8.19.1 Latin squares in experimental design
R methods:
***
Equivalent SPSS syntax:
***
8.19.2 The analysis of a basic Latin square
R methods:
***
Equivalent SPSS syntax:
***
8.19.3 A x B interactions in a single Latin square
R methods:
***
Equivalent SPSS syntax:
***
8.19.4 More subjects than rows: (a) using several squares
R methods:
***
Equivalent SPSS syntax:
***
8.19.5 More subjects than rows: (b) using one square several times
R methods:
***
Equivalent SPSS syntax:
***
8.19.6 BS designs using Latin squares (fractional factorial designs)
R methods:
***
Equivalent SPSS syntax:
***
8.19.7 Several-squares design with a BS factor
R methods:
***
Equivalent SPSS syntax:
***
8.19.8 Replicated-squares design with a BS factor
R methods:
***
Equivalent SPSS syntax:
***
8.20 Agricultural terminology and designs
R methods:
***
Equivalent SPSS syntax:
***
Test code
IN PROGRESS
References
- Sums of squares: for a very brief introduction see Cardinal (2010).
- Pros and cons of various types: http://afni.nimh.nih.gov/sscc/gangc/SS.html;
- J Fox, "?car::Anova" within R, or here;
- Langsrud (2003) "ANOVA for unbalanced data: Use Type II instead of Type III sums of squares", Statistics and Computing 13: 163-167;
- WN Venables (2000) Exeges on Linear Models.
- http://www.ats.ucla.edu/stat/r/faq/type3.htm
- http://myowelt.blogspot.com/2008/05/obtaining-same-anova-results-in-r-as-in.html
- J Baron & Y Li (2007) Notes on the use of R for psychology experiments and questionnaires.
- J Fox (2006) http://tolstoy.newcastle.edu.au/R/help/06/08/33529.html
- http://blog.gribblelab.org/2009/03/09/repeated-measures-anova-using-r/
- http://www.ats.ucla.edu/stat/R/seminars/Repeated_Measures/repeated_measures.htm
- http://www.personality-project.org/R/r.anova.html
- http://yatani.jp/HCIstats/ANOVA
- Re Greenhouse–Geisser and Huynh–Feldt episilons: R News, October 2007
- DC Howell (2009) "Statistical Methods for Psychology", fifth edition, Wadsworth.
- JL Myers & A Well (1995) "Research Design and Statistical Analysis", HarperCollins.
- J Fox (2010) https://stat.ethz.ch/pipermail/r-help/2010-March/230280.html
- WN Venables (2003) https://stat.ethz.ch/pipermail/r-help/2003-March/030705.html
- D Wollschläger, http://www.uni-kiel.de/psychologie/dwoll/r/ssTypes.php
- JL Myers & AD Well (2003). "Research Design and Statistical Analysis", second edition, Lawrence Erlbaum, New Jersey.
- SE Maxwell & HD Delaney (2004). "Designing Experiments and Analyzing Data: A Model Comparison Perspective", second edition, Lawrence Erlbaum, New Jersey.
-
On lme/lmer:



